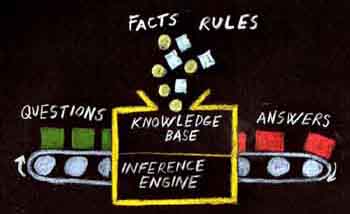
Pro/3 is a system for processing knowledge, and Pro/3 deals with two main categories of knowledge - facts and rules. The purpose of this page is to look at the concept of rules for inexact reasoning.
First of all - where do facts and rules come from? Facts and rules come from a knowledge engineer (KE for short), who either is an expert in the area of interest, or someone who has access to such an expert. The KE formulates the knowledge so that Pro/3 can make use of it in a way that makes the system produce something useful. Pro/3 supports two very different types of rules - sentence rules and rules for inexact reasoning. These two types differ in most respects: structure, usage and purpose; and they are handled by two different inference engines. Sentence rules are processed by a PROLOG-type inference engine (Pro/3's main inference engine), while rules for inexact reasoning are processed by a simpler inference engine called up by, but also making use of the main engine.  

Rules for inexact reasoning include certainty rules, fuzzy sets, support rules and data rules. All rule types return a simple value, i.e. a certainty factor or a probability in case of certainty rules, a membership grade in case of fuzzy sets, and these or any type of simple value in the case of support rules and data rules.

Certainty rules and fuzzy sets correspond to quite different sources of uncertainty. Certainty rules are typically used where the knowledge of the subject area is imprecise, while fuzzy sets are used where the knowledge classifications (knowledge concepts) are imprecise.

 

Certainty Factors

A certainty factor a is number in the range [-1,1] - a measurement of the certainty of a given proposition - the higher the certainty factor, the more true is the proposition, the lower the certainty factor, the more untrue is the proposition.

  • 1.0    true with absolute certainty
  • 0.5    true with quite high certainty 
  • 0.0    the evidence suggesting that the proposition is true is as good as the evidence suggesting that proposition is false
  • -0.5   false with quite high certainty
  • -1.0   false with absolute certainty

A certainty factor is generally considered as a relative, rather than an absolute, measure of certainty (this contrasts with probabilities which are absolute measurements - see also Probabilities - Conditional Probabilities and Certainty Factors). Certainty factors are thus suited for ranking propositions according to their certainty factors.

 

Fuzzy Sets Membership Grades
An essential assumption in traditional "crisp" logic is that something (an element belonging to a certain universe) either is a member of a given set or it is not a member, in which case it is a member of the complement set (in the universe). In fuzzy set theory this is not so. Fuzzy set membership is qualified by a degree of membership (called membership grade in Pro/3), given by the set's membership function, which is a mapping from an element (represented by a parameter or parameters) to a real number in the range [0,1]. This number is the membership degree, where 0 means that the element is definitely not a member of the set, 1 means that element definitely is a member of the set, while values in the range <0,1> mean that the element is a member to a degree. The higher the value, the higher the degree of membership. An element can both be a member of a fuzzy set and its complement.

 

Inexact Rules Semantics

A rule for inexact reasoning (in Pro/3) is a special type of function which returns a simple value (typically a certainty factor or membership grade). The function usually has one or more input parameters. The semantic interpretation of a reference (call) to the function is

in case of certainty rules:

the function and the actual parameter values is a proposition, and the returned certainty factor is a measurement of the certainty of this proposition

in case of fuzzy sets:

the function is a fuzzy set membership function, and the returned membership grade is the membership grade of the set element identified by the actual parameters   

The ultimate purpose of inexact rules in Pro/3 is to return a value to a data element in the conclusion of a sentence rule:

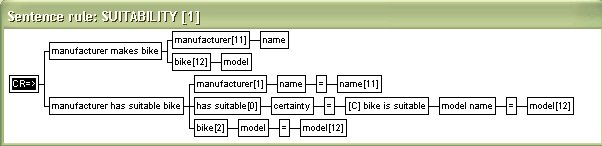
In the example above the certainty rule bike is suitable returns a certainty factor to the data element certainty in the manufacturer has suitable bike sentence type. For each manufacturer makes bike sentence, a manufacturer has suitable bike sentence is derived. These sentences state the certainty of the given manufacturer's bike model for being "suitable".
 

Rule Networks

An inexact rule is invariably only a part of a (complex) network of  rules calling each other. Inexact rules are mostly about calling other rules in various contexts, and combining or otherwise using the values returned from these called rules in different ways. The structure of rule calls forms a directed acyclic graph (rule network), with rules as graph nodes and calls as directed connectors (from the called rule to the calling rule i.e. the arrow is direction of returning values). 

With the sole exception of a group of rules called data rules, all inexact rules call at least one other rule. While data rules can do one type of rule calls known as context calls, they generally do not call other rules, and thus are terminal nodes in the graph. The purpose of a data rule is to return a value on the basis of either a query to the knowledge base (single value query), or by questioning the KE (user). Thus inexact rules derive the value they return in three ways:

  • by calling other certainty rules and combining or mapping these rules' returned values in various ways
  • by querying the knowledge base
  • by questioning the knowledge engineer

A inexact rule network always has one root node, that is, the certainty rule or fuzzy set called by a sentence rule (such as the bike is suitable rule in the example above). The evaluation of the rule network starts with this rule.

 
Example

Rule R1 calls R2, R3, and R4. R2 does not call any other rule, while R3 calls R4 and R5, and R4 finally calls R6. 

If R1 is the rule called by a sentence rule, then evaluation starts with this rule. However, the rules called by R1 must first be evaluated i.e. R2 ,R3 and R4. R2 can now be evaluated, however R4 and R5 must be evaluated before R3. R5 can be now be evaluated, while R6 must be evaluated before R4. R6 can now be evaluated followed by R4, followed by R3 and finally R1. 
 

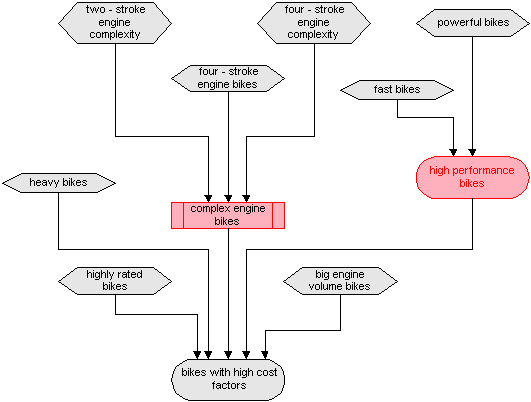
The diagram under shows a part of the rule network with has the fuzzy set bikes with high cost factors as root (not shown). The diagram is drawn via the MS Visio import format generated by Pro/3:

 

 
 

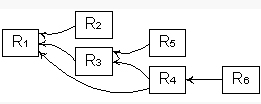
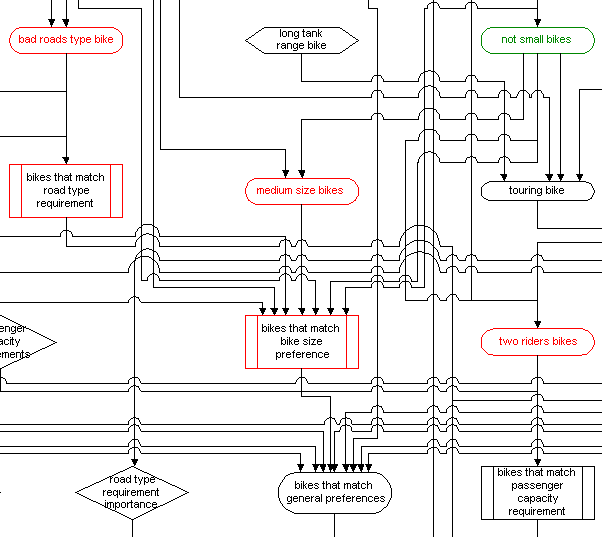
In most applications inexact rule networks tend to be complex and difficult to review in graph format, as is illustrated by a small part of the MC KB (under). The built-in tree drawing capability of Pro/3 is usually easier to use (see the complete inexact rule network for the MC KB).

 

 

INPUT PARAMETERS

An inexact rule has, usually, one or more (formal) input parameters. Formal parameters must be defined as data element types prior to being specified as parameters. The values of the actual parameter(s) in a call to a rule, impact the value returned by the rule in four different ways:

  • by being passed on to other rules called by the rule
  • by being embedded in a query to the KB processed by a query-type rule 
  • by being embedded in a question to the KE asked by a question-type rule
  • by being used as a criterion for selecting a rule within a switch-type rule

Note!

Actual parameters of certainty rules can only be simple values, i.e. literal values or variables (parameters). Expressions can not be used as actual parameters for certainty rules.

Types of Inexact Rules

Inexact rules can be dividend into four groups: certainty rules, fuzzy sets, support rules and data rules.  The support rules manipulate the flow in the inexact rule network, while the data rules retrieve relevant information from the user or from the knowledge base. 

GROUP

TYPE

DESCRIPTION

 RETURN DOMAIN
CERTAINTY

RULES

 Bayesian A bayesian-type function returns a certainty factor (or probability) by applying assumptions (built in to the rule) of dependent probabilities on the certainty factors (or probabilities) returned by one ore more called rules (which return probabilities (or certainty factors)), by applying assumptions (built in to the rule) of dependent probabilities (see Probabilities - Dependent Probabilities - Certainty Factors ). certainty factor (also probability via certainty factor)
Combination Returns a certainty factor (or probability) from two or more called rules (which return certainty factors (or probabilities)), according to the following formula:
  • CF1>0,CF2>0 : CF1+CF2 - CF1*CF2 
  • CF1<0,CF2<0 : CF1+CF2 + CF1*CF2 
  • CF1=-CF2 ,CF1+CF2 =0: 0
  • else : (CF1+CF2) / (1-min(|CF1|,|CF2|))

(see also Probabilities - Dependent Probabilities - Certainty Factors ).
AND Returns the lowest of the returned probabilities or certainty factors of two or more called rules. (The probabilities will be used if the the rule returns a probability and vice versa). certainty factor or probability
OR Returns the highest of the returned probabilities or certainty factors of two or more called rules. (The probabilities will be used if the the rule returns a probability and vice versa). 
NOT Returns the inverse probability (or certainty factor) of another rule. (The probabilities will be used if the the rule returns a probability and vice versa). The inverse of probability p is 1-p. The inverse of certainty factor c is computed by first computing pc (the probability corresponding to c - see prior probabilities), and then computing the certainty factor ci corresponding to 1-pc.
FUZZY SETS Complement The membership function for the complement of a fuzzy set. membership grade
Intersection The membership function for the intersection of two or more fuzzy sets (by using one of the four intersection methods standard intersection, algebraic product intersection, bounded difference intersection or drastic intersection).
Union The membership function for the union of two or more fuzzy sets (by using one of the four union methods standard union, algebraic product union, bounded difference union or drastic union).
Ordered Weighted Averaging The membership function for a set averaging operation of one or more fuzzy sets, where a weighting factor is applied to the contributing sets.

SUPPORT

RULES

 Switch Returns the value returned from a called rule selected from a list of rules, on the basis of a call to a special "switch" certainty rule (call-switch type switch rule). Comparison is made to a switch-type of statement used in various programming languages. any non-list domain
Returns the value returned from a called rule selected from a list of rules, on the basis of one of the rule's input parameters (parameter-switch type switch rule).
Parameter Calls one or more rules and uses the values returned by these rules as actual parameters in a call to another rule. The value returned by this last rule is the value returned by the rule.
Map Returns a value mapped from another value (returned from a called rule).
DATA RULES Query Returns a value by querying the knowledge base (single-value query). The query can be parameterized, such that one or more of the input parameters to the rule can be used as actual parameters in the query. The answer to the query can optionally be mapped into another value through a defined map which forms a part of the rule. any non-list domain
Question Returns a value by soliciting a value from the user during the interpretation of the rule. The question text associated with the rule, can be parameterized such that one or more of the rule's input parameter values can be used as part of the question text. The answer to the question can optionally be mapped into another value through a defined map which forms a part of the rule.  

 

Prior Probability and Context in Certainty Rules

A certainty rule's prior probability is a probability stating that prior to the evaluation of the rule, the probability that the statement is true is such and such. The prior probability is accordingly a number in the range [0.0 ... 1.0], in reality <0.0 ...1.0> as certainty rules with a prior probability of 0 or 1 would not have any practical use in a problem-solving model. 

Prior probability is only meaningful for rules that return a certainty factor or a probability. (Prior probability is not entered for other rules, however since all stored rules (rule records) have a prior probability element, the value of 0.5 is used as a dummy. This value has no significance when evaluating the rule or the rule network).

For more in-depth explanation of the relationship between certainty factors, probabilities and bayesian-type rules, refer to Probabilities - Dependent Probabilities - Certainty Factors ).

 

The correspondence between a certainty factor and probability, is as follows (Pp is the prior probabilityI):

 

PROBABILITY   P CERTAINTY   C
P = 0 -1
P = 1 1
P <=  Pp ( P / Pp ) - 1
P >  Pp ( P - Pp ) / ( 1 - Pp )
CERTAINTY  C PROBABILITY  P
C <=  0 Pp * ( C + 1 )
C > 0 Pp + ( 1 - Pp ) *C

 

All inexact rules except fuzzy sets, can optionally have a context. A context is simply one or more calls to other rules (of any type). Each call is associated with a condition (such as a value range), which applies to the value returned by the called rule. If at least one of the returned values  violate the specified condition, then the calling rule is considered out of context and the rule's  out of context value is returned.

 

Fuzzy set concepts
For definitions and illustrations of fuzzy set concepts, refer to Fuzzy Set Concepts.
 

RETURN VALUES IN EXCEPTION SITUATIONS

Inexact rules never fail to return a value, and exception-situations are handled as follows:
EXCEPTION SITUATION HANDLING
Query in query-rule fails to return a value. The specified default value is used in place of the value otherwise returned by the query (which must agree in domain).
User cancels question-dialog in question rule. The specified default value is used in place of the value otherwise returned by the user (which must agree in domain).
The value returned by the criterion-rule in a call-type switch-rule does not determine any of the switch branches. The specified default criterion value is used in place of the value returned by the criterion rule (which must agree in domain).
The actual parameter value in a parameter-type switch-rule does not determine any of the switch branches. The specified default criterion value is used in place of the actual parameter (which must agree in domain).
   
While numeric maps (used in map-rules and optionally in query- and question-rules), can map any value (as long as the domain is numeric), discrete maps can only map a limited set of values. This means that discrete maps could fail if the value attempted mapped is outside the set. Pro/3 will in such cases attempt to map the predefined default value. Consequently, mapping will always succeed (under the assumption that the default value is map-able). Cases with unmappable default values are considered rule definition errors. They can give rise to run-time errors during rule interpretation). 

See Using Inexact Rules in Pro/3 for a more detailed explanation of inexact rules and their usage in Pro/3.
 

Evaluating Inexact Rules

Three questions crop up when working with inexact rule-based reasoning models:

  • Are the answers given trustworthy/valid?
  • Why is the model giving a certain answer i.e. what is the detailed reasoning behind it?
  • How can the rules (the rule network - the model) be improved? 

These and related issues are discussed in the topic Validating the Model.