|
An essential assumption in traditional "crisp"
logic is that something (an element belonging to a certain universe)
either is a member of a given set or it is not a member, in
which case it is a member of the complement set (in the universe).
In fuzzy set theory this is not so. Fuzzy set membership is qualified by a
degree of membership, given by the set's membership function,
which is a mapping from an element (represented by a parameter or
parameters) to a real number in the range [0,1]. This number is the
membership degree, where 0 means that the element is not a member of
the set, 1 means that element definitely is a member of the set, while
values in the range <0,1> mean that the element is a member to
a degree. The higher the value, the higher the degree of membership. An
element can both be a member of a fuzzy set and its complement.
Fuzzy sets are named A, B, C, ... in
this topic, while their associated membership functions are named FA,
FB, FC ... Parameters which determine whether or
not an element is member of a set are called x, y, z, ...FA(x)
is the degree to which x is a member of A.
|
| CONCEPT |
NOTATION |
DEFINITION |
| alpha-cut
of FA |
aFA |
{ x | FA(x)
>= a } |
| strong
alpha-cut of FA |
a+FA |
{ x | FA(x)
> a } |
| support
of A |
|
0+FA |
| core
of A |
|
1FA |
| level
set of A |
L(A) |
{ a |
exists x such that FA(x)=a } |
| height
of A |
h(A) |
max(A(x))
for all x in 0+FA. |
| A
is normal |
|
h(A)=1
|
| A
is sub-normal |
|
h(A)<1 |
|
standard
complement of A |
FA^(x) |
1-FA(x). |
| averaging
operation |
|
An operation
on A, B, C, ... such that min(FA(x),FB(x),FB(x),...)
<= (FA op FB op FC...)(x)
>= max(FA(x),FB(x),FB(x),...) |
|
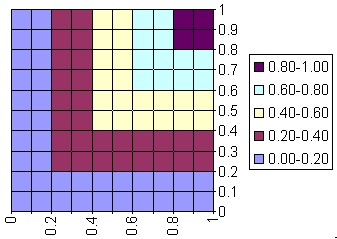
standard
intersection1 of A and B |
(FA&FB)(x) |
min(FA(x),FB(x)) |
 |
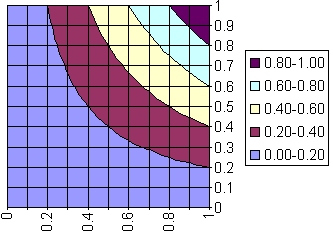
| algebraic
product intersection1 |
(FA&apFB)(x) |
FA(x)*FB(x) |
 |
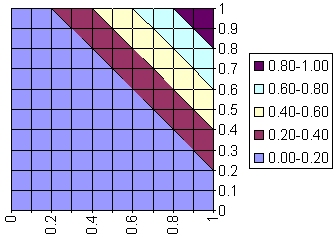
| bounded
difference intersection1 |
(FA&bdFB)(x) |
max(0,FA(x)+FB(x)-1) |
 |
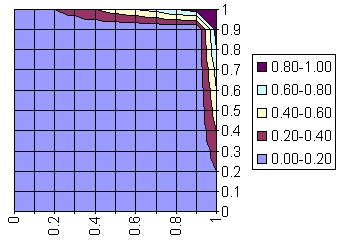
| drastic
intersection1 |
(FA&dFB)(x) |
- FB(x)=1: FA(x)
- FA(x)=1: FB(x)
- else: 0
|
|
|
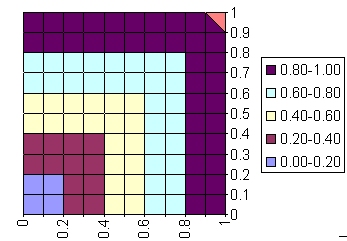
standard
union1 between A and B |
(FAUFB)(x) |
max(FA(x),FB(x)) |
 |
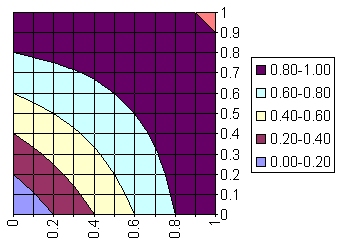
| algebraic
sum union1 |
(FAUasFB)(x) |
FA(x)+FB(x)-FA(x)*FB(x) |
 |
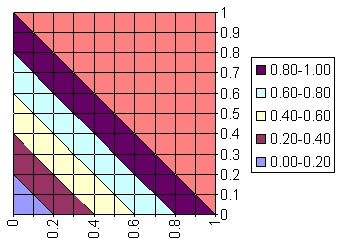
| bounded
sum union1 |
(FAUbsFB)(x) |
min(1,FA(x)+FB(x)) |
 |
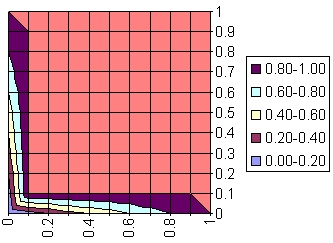
| drastic
union1 |
(FAUdFB)(x) |
- FB(x)=0: FA(x)
- FA(x)=0: FB(x)
- else: 1
|
|
|
ordered
weighted averaging |
FOWA(x) |
The ordered weighted averaging
operation is associated with a weighting vector w=(w1,w2,...wN)
where sum Ni=1 wi = 1.0. FOWA(x)=w1*F1(x)+w1*F2(x)+...+w1*FN(x).
|
|
Notes:
-
Intersection and
union operations are commutative such that e.g. (FAUFB)(x)=(FBUFA)(x),
and associate such that e.g. (FA&(FB&FC))(x)=((FA&FB)&FC)(x).
|
|







